CINÉTIQUE DES FLUIDES (THÉORIE)

CINÉTIQUE DES FLUIDES (THÉORIE)

La théorie cinétique des fluides appartient à une branche de la physique qui se propose d’expliquer les propriétés macroscopiques des fluides à partir d’une analyse statistique des mouvements des particules qui les constituent. On peut classer les fluides en trois grandes familles: gaz, liquides, plasmas.

Les gaz sont constitués de molécules neutres en faible concentration: les molécules y sont éloignées les unes des autres et se meuvent en général en ligne droite. Plus précisément, la trajectoire d’une molécule est une ligne brisée constituée de segments, le long desquels la molécule se meut librement, raccordés par des coudes brusques qui se produisent quand deux molécules se rencontrent (collision binaire).

Les liquides sont constitués de molécules neutres en forte concentration, pratiquement au contact les unes des autres; elles sont en interaction permanente avec plusieurs molécules voisines. Les forces d’interaction à courte portée étant violemment répulsives, un liquide est un fluide très peu compressible.

Les plasmas sont constitués en tout ou en partie de particules électriquement chargées (électrons, ions positifs). On les obtient spontanément en chauffant la matière à des températures de l’ordre de 10 000 degrés. Les interactions entre particules chargées sont régies par la loi de Coulomb (potentiel d’interaction en 1/r ) et la décroissance très lente de ce potentiel en fonction de la distance confère aux plasmas des propriétés particulières: interactions lointaines et multiples dominantes, effets «collectifs».

Le point de départ de la théorie cinétique est l’analyse des collisions binaires entre deux particules. On distingue les collisions élastiques qui ne changent pas l’état interne des particules, et les collisions inélastiques qui changent celui d’au moins l’une des particules en jeu. La probabilité d’une espèce de collision donnée entre deux particules est précisée par une grandeur appelée section efficace qui dépend en général de la nature des deux particules, de leur vitesse relative et, bien sûr, de l’espèce de collision considérée. Dans les gaz à température peu élevée, les collisions élastiques sont dominantes.

Dans le formalisme classique de la théorie cinétique des gaz, on assimile chaque molécule à une masse ponctuelle dont le mouvement est, à un instant donné, défini par un vecteur position r et un vecteur vitesse w et on suppose que ces molécules interagissent par des forces centrales. Cette description s’applique bien aux gaz monoatomiques, mais elle doit être corrigée dans les autres gaz pour tenir compte des rotations et des vibrations des molécules.

Compte tenu du très grand nombre de molécules contenues en général dans un petit volume de gaz, on doit se contenter, pour décrire l’état microscopique du gaz, d’expressions statistiques qu’on appelle les fonctions de distribution des vitesses (fonction de distribution simple f ¹, double f ¹², ..., densité dans l’espace des phases D). Les lois de la mécanique permettent d’établir les équations d’évolution de ces grandeurs. Ce sont les équations cinétiques (équation de Boltzmann pour f ¹, équation de Liouville pour D).

À partir des fonctions de distribution des vitesses, on peut calculer par une méthode dite régressive les grandeurs mesurables à l’échelle macroscopique (grandeurs hydrodynamiques ): densité, vitesse moyenne de fluide, pression et température cinétiques, pression intermoléculaire, flux de molécules sur une paroi, flux de chaleur, fréquences de collision, et taux de réactions dans le cas des gaz chauds où se produisent des réactions physico-chimiques.

On peut également définir le libre parcours moyen entre deux collisions, et la comparaison de cette longueur aux dimensions du récipient permet de distinguer des régimes moléculaires (collisions dans la masse du gaz négligeables) et des régimes de fluide quasi continu (collisions dans la masse du gaz très fréquentes). Pour l’étude de ces derniers régimes, les grandeurs hydrodynamiques fournissent une description plus simple que les fonctions de distribution des vitesses.

Les équations d’évolution des grandeurs hydrodynamiques (équations hydrodynamiques ou équations de transport ) sont souvent écrites directement par application, au niveau macroscopique, des méthodes de la mécanique des milieux continus. Cependant, il est préférable de déduire les équations hydrodynamiques des équations cinétiques; cette déduction rigoureuse met en évidence les approximations que contiennent les équations hydrodynamiques: on s’aperçoit ainsi que ces équations forment a priori un système infini et que, pour les utiliser, il faut trouver une méthode de fermeture de ce système, fondée sur des considérations physiques. Cette analyse permet, en outre, de calculer, à partir des lois d’interaction entre molécules, les coefficients de transport tels que la viscosité et la conductibilité thermique, qui apparaissent au niveau des équations hydrodynamiques comme des propriétés caractéristiques du fluide considéré.

1. Collisions binaires entre atomes et molécules

Dans un fluide dilué, tel qu’un gaz à basse pression, il peut arriver que deux atomes ou molécules se rapprochent exceptionnellement à une distance de l’ordre des dimensions atomiques (quelques angströms), et il se produit alors un phénomène d’interaction plus ou moins violente, qu’on appelle une collision binaire. On distingue deux familles de collisions binaires: les collisions élastiques et les collisions inélastiques. Dans un fluide dilué, le rapprochement de trois particules à des distances de l’ordre des dimensions atomiques (collision ternaire) est un phénomène hautement improbable.

Collision binaire élastique

Pour décrire une collision binaire élastique, on peut tout d’abord utiliser les méthodes de la mécanique classique, non relativiste. On assimile les deux particules qui entrent en collision à des masses ponctuelles qui interagissent par l’intermédiaire d’une force centrale dérivant d’un potentiel 淋(r ); celui-ci ne dépend que de la distance r entre les deux particules 1 et 2. On obtient alors les résultats suivants:

– Le centre de gravité des deux particules est animé d’un mouvement rectiligne uniforme de vitesse w^G.

– Le mouvement des deux particules peut être considéré comme la composition du mouvement rectiligne du centre de gravité G et du mouvement relatif des deux particules par rapport à G.

– Quand les forces d’interaction sont des forces centrales, le mouvement relatif est un mouvement plan.

– L’énergie cinétique T du système des deux particules peut, à tout instant, être considérée comme la somme de l’énergie cinétique ^g du centre de gravité et de l’énergie cinétique ^r du mouvement relatif.

– L’énergie cinétique ^G est égale à Mw ^G2/2, où M = m ¹ + m ² est la masse totale du système des deux particules; elle reste constante pendant toute la collision.

– L’énergie cinétique relative ^r est égale à 猪g ²/2, où g est la vitesse relative w¹ 漣 w² du système des deux particules et 猪, appelée masse réduite , est donnée par la formule:

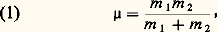– Dans une collision élastique, l’énergie cinétique relative ^r retrouve à la fin de la collision sa valeur initiale; il en va de même de la vitesse relative g . L’effet de la collision élastique est donc simplement de faire subir au vecteur vitesse relative w¹ 漣 w² une certaine rotation.

– La géométrie d’une collision peut donc finalement se représenter comme il est indiqué sur la figure 1. On y fait abstraction du mouvement de G, c’est-à-dire que l’on décrit, dans un système de coordonnées liées au centre de gravité, le mouvement relatif des deux particules 1 et 2. Dans ce mode de représentation, longtemps avant la collision, les deux trajectoires sont deux droites parallèles séparées par une distance p appelée paramètre d’impact ; les deux trajectoires suivies par les deux particules sont homothétiques par rapport au point G. Après la collision, les deux trajectoires asymptotiques sont à nouveau des droites parallèles distantes de p ; la direction de ces asymptotes après la collision est repérée par deux angles: l’angle de déviation 﨑 et un angle d’azimut 﨏 mesuré par rapport à un axe quelconque dans le plan perpendiculaire à la vitesse relative initiale (fig. 1).

– Pour étudier le mouvement relatif, on peut remplacer le problème à deux corps représenté sur la figure 1 par un problème à un seul corps dans lequel un mobile fictif de masse 猪 tourne autour d’un point fixe O; le vecteur position relative étant défini comme r = r¹ 漣 r², et l’action du centre fixe O étant définie par le même potentiel d’interaction 﨏(r ) que précédemment, on a la représentation indiquée sur la figure 2, tracée dans le plan du mouvement relatif.

– La grandeur fondamentale dans les calculs de théorie cinétique est l’angle de déviation 﨑; elle s’obtient à partir des valeurs de g , p et du potentiel d’interaction 﨏(r ) par la formule générale:

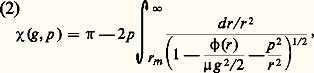où r ^m , distance de plus courte approche (fig. 1), est le plus grand zéro de la quantité entre crochets.

Potentiels d’interaction

Pour pouvoir analyser les phénomènes de collision élastique dans un fluide dilué, il faut donc connaître la loi d’interaction 﨏(r ), et l’on considère alors divers cas selon la nature du fluide observé:

– Dans un plasma complètement ionisé, toutes les particules ont une charge électrique, et l’énergie potentielle d’interaction entre une particule de charge Z¹e et une particule de charge Z²e est:

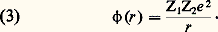– Dans un gaz partiellement ionisé , on a souvent à considérer les collisions entre une particule chargée (électron ou ion) et une particule neutre (atome ou molécule); dans ce cas, on peut montrer qu’à grande distance la force d’interaction est attractive et l’énergie d’interaction est donnée par la formule:

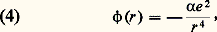où 見 est la polarisabilité de la molécule. Cette interaction peut s’expliquer par un raisonnement simple d’électrostatique: la particule chargée polarise électriquement la particule neutre et y crée un petit dipôle électrique; ce dipôle induit est alors soumis à une force résultante attractive (fig. 3). Lorsque les deux particules s’approchent à des distances de l’ordre des rayons atomiques, cette description classique n’est plus valable; des forces d’origine quantique très intenses et généralement répulsives apparaissent.

– Dans un gaz neutre , les forces à considérer sont celles qui existent entre atomes neutres ou molécules. Les potentiels sont en général assez mal connus malgré de nombreux travaux récents. De manière générale, la loi 﨏(r ) a alors l’allure représentée sur la figure 4: à grande distance, on a une attraction avec 﨏(r ) 黎 漣 A/r ⁶; ce type de force, dit de Van der Waals , est dû à l’interaction moyenne entre le dipôle instantané de l’un des atomes et le dipôle induit dans l’autre; à courte distance apparaissent des forces quantiques intenses et généralement répulsives qu’on représente parfois par une loi 﨏(r ) = + B/r ¹² et parfois par des lois exponentielles.

– On représente souvent les interactions entre deux atomes neutres, ou entre une particule chargée et un atome, en adoptant le modèle simplifié dit des boules de billard (ou des sphères dures ). Dans ce modèle (fig. 4, courbe 2), on néglige complètement les interactions à grande distance et on suppose qu’une force répulsive infinie apparaît pour une certaine distance critique r = D.

Section efficace de collision élastique

En pratique, il est impossible de déterminer dans une expérience tous les paramètres cinétiques et géométriques représentés sur la figure 1: en particulier à l’échelle atomique le paramètre d’impact p est une grandeur qui n’est pas directement accessible à l’expérience; en analysant ce problème du point de vue de la mécanique quantique, on s’aperçoit facilement qu’il s’agit même là d’une indétermination fondamentale imposée par le principe de Heisenberg. C’est pourquoi on est amené à introduire dans la description des collisions des méthodes statistiques, en utilisant la notion de section efficace.

On peut tout d’abord considérer l’expérience représentée sur la figure 5, dans laquelle un faisceau de particules monocinétiques 1 vient bombarder une particule cible 2, et ces particules subissent, sur la cible, des collisions élastiques. Pour la commodité du raisonnement, on peut supposer que la particule 2 a une masse infinie et qu’elle est donc immobile (en fait cela revient, dans le cas général où m ² est finie, à décrire le mouvement relatif en considérant des mobiles fictifs de masse 猪; fig. 2). Pour éliminer la grandeur non mesurable qu’est le paramètre d’impact , on peut, tout en gardant la description classique, considérer que les particules sont réparties au hasard dans la section droite du faisceau. On peut aussi, cela revient au même et c’est théoriquement plus satisfaisant, adopter le point de vue de la mécanique quantique et considérer que le faisceau incident constitue une onde plane monochromatique, qui va être partiellement diffusée par la particule cible 2. Quoi qu’il en soit, il y a une diffusion des particules dans toutes les directions et on peut mesurer le nombre de particules d ¹/dt diffusées par unité de temps dans un petit angle solide d 行 centré sur une direction repérée par les deux angles 﨑 et 﨏 (fig. 5); on pose alors par définition:

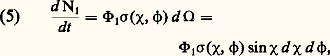où 淋¹ est le flux (nombre de particules, par unité de temps et par unité de surface) transporté par le faisceau incident. La quantité 靖( 﨑, 﨏)d 行 a les dimensions d’une surface; on l’appelle section efficace différentielle de collision élastique. À partir de cette grandeur, on peut définir des sections efficaces intégrales:

– section efficace «totale»

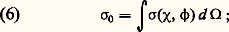– section efficace pour le transfert de quantité de mouvement

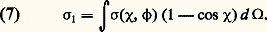Le calcul de 靖( 﨑) doit en principe être fait par les méthodes de la mécanique quantique en résolvant l’équation de Schrödinger du système des deux particules. On peut également obtenir les sections efficaces par diverses méthodes expérimentales; la figure 6 montre à titre d’exemple les variations de 靖¹ en fonction de l’énergie pour la diffusion élastique des électrons sur l’atome d’argon.

Le tableau 1 donne les expressions de 靖( 﨑), 靖⁰ et 靖¹ dans deux cas limites : modèle des boules de billard et interaction coulombienne. Ces deux cas sont limites, en ce sens que le premier représente le potentiel à variation la plus rapide avec r que l’on puisse imaginer et peut servir comme nous l’avons déjà vu de modèle approché pour les forces à courte portée entre deux atomes ou molécules neutres, alors que le second, que l’on rencontre dans les gaz ionisés, est au contraire le potentiel à variation la plus lente avec r. Dans ce deuxième cas, on peut vérifier que les interactions lointaines sont statistiquement dominantes; ce sont elles qui rendent 靖⁰ infini, ce qui, a priori, n’est pas gênant car 靖⁰ n’a en général aucun sens expérimental. La quantité 靖¹ a, au contraire, un sens physique précis, car elle permet de calculer la force moyenne F exercée par le faisceau sur la particule cible 2 , au moyen de la formule:

Un calcul brutal utilisant la formule (7) donne cependant dans le cas du potentiel coulombien 靖¹ = 秊. Cette difficulté, due à l’importance des collisions lointaines, peut être levée en tenant compte des phénomènes d’interaction multiple (effets collectifs); on est alors conduit au facteur correctif Log 炙 appelé logarithme coulombien qui figure dans le tableau 1; ce facteur est en général compris entre 1 et 20.

Collisions inélastiques

Une collision inélastique se produit avec changement des états internes des particules, et parfois apparition ou disparition de particules: collision inélastique est donc synonyme de réaction physico-chimique et on explicite en général une telle réaction au moyen de l’une des deux notations suivantes:

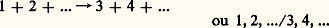où 1, 2, ... sont les particules qui existent avant la collision (par exemple deux atomes dans le niveau fondamental) et 3, 4, ... les particules qui existent après la collision (par exemple un atome excité, un ion positif et un électron). Dans une collision inélastique, il y a conservation de l’énergie du centre de gravité mais variation de l’énergie interne des particules et de l’énergie cinétique du mouvement relatif qui augmente d’une quantité Q positive ou négative appelée énergie de réaction. Si Q est négatif, la réaction est endoénergétique et l’on dit qu’on a une collision de première espèce ; si Q est positif, la réaction est exoénergétique et l’on dit qu’on a une collision de deuxième espèce (ou superélastique ). Les réactions endoénergétiques ne peuvent se produire que si l’énergie cinétique ^r du mouvement relatif satisfait à la condition de seuil :

Le tableau 2 indique les types de collisions inélastiques les plus importants qui peuvent se produire dans un gaz.

Généralisation de la notion de section efficace

Pour préciser la probabilité de tel ou tel type de collision inélastique, on généralise pour toute collision binaire la notion de section efficace en considérant l’expérience représentée sur la figure 7, c’est-à-dire l’action d’un faisceau monocinétique de particules d’espèce 1, sur une cible mince d’épaisseur dx constituée de particules d’espèce 2 en densité n ² (nombre de particules / unité de volume) et supposée ici au repos (on verra plus loin comment tenir compte dans un gaz de l’agitation thermique des particules d’espèce 2). On peut alors considérer une certaine réaction susceptible de se produire (par exemple l’ionisation des particules 2) et compter le nombre d ¹ d’événements de ce type qui se sont produits lorsque le faisceau incident a apporté ¹ particules 1, et l’on écrit la probabilité de la réaction considérée d ¹¹ sous la forme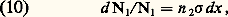

où 靖 qui a les dimensions d’une surface est la section efficace pour la réaction considérée. Pour appliquer cette formule directement il faut d’ailleurs que dx soit assez faible pour que la probabilité de réaction d ¹¹ soit nettement inférieure à l’unité (sinon des effets de réactions multiples compliquent le phénomène). On peut vérifier pour les collisions élastiques que les deux définitions (5) et (10) sont équivalentes, mais la définition (10) est plus générale et s’applique à toutes les espèces de collisions inélastiques; 靖 est en général fonction de la vitesse relative g , c’est-à-dire de l’énergie du mouvement relatif. On trouve, dans divers ouvrages, des tables de valeur des sections efficaces les plus importantes. En général, pour une réaction endoénergétique, la courbe de 靖 en fonction de l’énergie relative ^r a l’allure représentée sur la figure 8: croissance à partir du seuil, passage par un maximum puis décroissance régulière. Notons enfin que, pour toute réaction et pour un faisceau monocinétique, on peut à partir de la relation (10) définir une fréquence de collision et un libre parcours moyen dans la cible par les formules:

Ces deux grandeurs sont en général des fonctions de g .

2. Fonctions de distribution des vitesses

Les molécules constituant un gaz sont animées à tout instant de mouvements désordonnés qui constituent ce qu’on appelle l’agitation thermique. La description fine d’un gaz doit donc tenir compte de cet état microscopique; cependant un petit volume de gaz contient toujours en pratique un très grand nombre de molécules (1mm³ d’air dans les conditions normales contient 2,7 . 10¹⁶ molécules); c’est pourquoi, pour décrire l’état microscopique du gaz, on doit se contenter d’expressions statistiques qu’on appelle les fonctions de distribution des vitesses et qui sont les grandeurs de base de la théorie cinétique des gaz.

Fonction de distribution simple

À un instant donné, le mouvement d’une molécule du gaz peut être caractérisé par son vecteur position r et son vecteur vitesse w. On représente la position par un point dans l’espace ordinaire et le vecteur vitesse par un point dans l’espace des vitesses. Dans chacun de ces deux espaces, on considère alors deux petits éléments de volume dr 漣 = dx dy dz et dw 漣 = dw ^x dw ^y dw ^z, centrés respectivement autour des valeurs moyennes r et w de la position ou de la vitesse. On désigne par 麗d N 礪 le nombre probable de molécules du gaz dont les points représentatifs sont dans dr 漣 , en ce qui concerne la position, et dans dw 漣 , en ce qui concerne la vitesse; ce nombre est évidemment proportionnel à dr 漣 et dw 漣 et l’on posera par définition: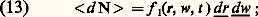

f ¹ (r, w, t ) est appelée la fonction de distribution simple des vitesses (on omet souvent l’adjectif «simple», quand il n’y a pas d’ambiguïté). Une fonction de distribution peut être:

– stationnaire , si elle ne dépend pas de t ;

– homogène , si elle ne dépend pas de r;

– isotrope , si elle ne dépend que du module de w et non de son orientation.

La figure 9 représente un cas de distribution instationnaire, inhomogène, anisotrope obtenue par l’injection d’une bouffée de gaz dans un récipient préalablement vidé.

En pratique, on applique généralement la relation de définition (13) à des éléments de volume qui, tout en étant petits à l’échelle macroscopique, sont encore assez grands pour contenir un grand nombre de molécules. Dans ces conditions, la loi des grands nombres permet d’affirmer que le nombre réel d N de molécules contenues dans ces éléments de volume est voisin du nombre probable 麗d N 礪 et l’on omet alors dans (13) le signe 麗礪. Quoi qu’il en soit, la fonction de distribution simple permet de calculer presque toutes les grandeurs macroscopiquement mesurables (densité, vitesse de fluide, pression cinétique, taux de réactions physico-chimiques...).

Fonction de distribution double

Pour l’étude de certaines propriétés des gaz, on a besoin de connaître les corrélations binaires entre deux points 1 et 2, c’est-à-dire de savoir dans quelle mesure ce qui se passe au point 1 est affecté par ce qui se passe au point 2 et réciproquement. Considérant donc deux points 1 et 2, définis par leurs positions r¹, w¹ et r², w² dans l’espace ordinaire (espace des positions) et dans l’espace des vitesses, on leur associe de petits éléments de volume dr 漣 ¹, dw 漣 ¹, dr 漣 ², dw 漣 ² centrés respectivement sur r¹, w¹ et r², w². Cela étant, on désigne par 麗d ² 礪 le nombre probable de couples de particules dont les points représentatifs sont dans dr 漣 ¹ dw 漣 ¹ pour la première particule du couple, et dans dr ² dw ² pour la deuxième, et on pose par définition:

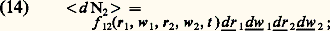f ¹² (r¹, w¹, r², w², t ) est appelée la fonction de distribution double (par convention on choisit en général dans le décompte de d ², de compter chaque couple 見廓 deux fois; une fois en désignant par 見 la particule située en 1, et une fois en désignant par 見 la particule située en 2).

Lorsque les points 1 et 2 sont suffisamment éloignés dans l’espace des positions, on a:

en désignant par f ¹ et f ² les valeurs de la fonction de distribution simple aux points 1 et 2. Dans ces conditions, la probabilité double f ¹² se réduit à un produit de probabilités simples, et l’on dit que les corrélations sont négligeables ou encore qu’entre deux points suffisamment éloignés le fluide obéit à la règle du chaos moléculaire. En dessous d’une certaine distance qu’on peut appeler la longueur de corrélation et qui dépend des interactions entre particules, la loi (15) n’est plus valable: il y a des corrélations; par exemple, s’il existe d’importantes forces de répulsion à courte distance, f ¹² doit tendre vers zéro quand la distance entre les points 1 et 2 tend vers zéro.

Densité dans l’espace des phases

En généralisant les notions introduites ci-dessus, on peut définir des fonctions de distribution triples f ¹²³, quadruples f ¹²³⁴, ..., qui fournissent une description de plus en plus fine du système. Pour les études théoriques fondamentales de mécanique statistique et de théorie cinétique, on pousse cette description à l’extrême limite, en considérant une fonction de distribition à N particules où N est le nombre total de particules dans le système qu’on suppose donc fini et enfermé, par exemple dans un récipient de volume V (le passage à la limite V et N infinis avec N/V fini est étudié par certains auteurs). L’état ou phase d’un tel système gazeux constitué de N molécules toutes identiques peut donc être considéré comme complètement déterminé à un instant donné par la connaissance de la position et de la vitesse de chacune des N molécules, c’est-à-dire des variables r¹, w¹, r², w², ..., r^N, w^N, soit 6 N variables scalaires. On considère alors l’espace à 6 N dimensions constitué avec ces variables: on l’appelle l’espace des phases. Un élément de volume de cet espace des phases s’écrit symboliquement: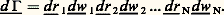

L’information la plus fine que l’on puisse obtenir sur l’état du système est la probabilité pour que sa phase se trouve dans un tel élément d 淋 centré sur un point moyen r¹, w¹, r², w², ..., r^N, w^N de l’espace des phases, et par définition on écrit cette probabilité sous la forme:

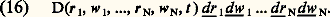La fonction D est appelée densité dans l’espace des phases.

Si l’on connaît D, on peut en déduire toutes les fonctions de distribution par une méthode dite régressive qui consiste à perdre de l’information par une série d’intégrations. Plus précisément on a:

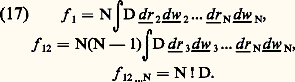Dans ces formules, les intégrations sur les variables de position sont étendues au volume V du récipient, et les intégrations sur les vitesses à tout l’espace des vitesses concerné.

3. Grandeurs macroscopiques et fonctions de distribution

Dans les études macroscopiques de fluides (hydrodynamique et physico-chimie), on définit un certain nombre de grandeurs macroscopiques (densité, vitesse de fluide, pression...). Chacune d’entre elles est supposée directement mesurable par une expérience typique; par exemple, la pression est définie à partir de la force normale agissant sur une paroi. Ces définitions macroscopiques cachent cependant parfois des difficultés et on adoptera ici le point de vue qu’on peut définir les grandeurs macroscopiques à partir des fonctions de distribution; en cela, on poursuit la méthode régressive qui a permis de passer de D à f ¹. Bien entendu, ces définitions sont choisies de manière à recouper dans les cas simples celles de l’hydrodynamique élémentaire.

Densité simple et double

La densité simple (nombre de molécules par cm³) est définie par la formule:

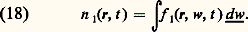Comme toutes les grandeurs macroscopiques, la densité simple est une fonction de r et de t et non de la vitesse microscopique w, celle-ci s’étant éliminée dans l’intégration (18).

La densité double (dont on se servira pour évaluer l’effet macroscopique des interactions entre molécules) est définie par:

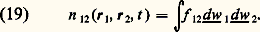Dans un fluide homogène isotrope, elle ne dépend que de la distance r ¹² = |r¹ 漣 r²|.

Vitesse de fluide

La vitesse de fluide v est la valeur moyenne de w pondérée par la fonction de distribution simple. Soit:

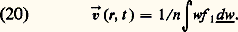Dans un fluide au repos, 轢v est nulle; dans les écoulements lents usuels (subsoniques ), la vitesse de fluide est bien plus petite en valeur absolue que les vitesses d’agitation thermique w (face=F0019 轢v plus petit que la moyenne de |w|); dans de tels écoulements le fluide reste donc presque isotrope.

Flux de molécules dans un gaz isotrope

Dans un gaz isotrope, le flux qui traverse un élément de surface placé en un point quelconque du fluide est nul; mais il est en fait la somme algébrique de deux flux égaux 淋 et 淋 traversant la surface en sens contraire. Le calcul de ces flux à partir de f ¹ donne la formule générale:

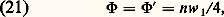où w ¹ est la valeur moyenne de |w|, c’est-à-dire:

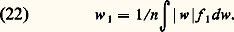La formule (21) a de nombreuses applications, car on peut l’appliquer (fig. 10) non seulement à une paroi imaginaire située dans la masse du gaz, mais aussi à une paroi réelle (étude des phénomènes d’adsorption ), ou à un trou dans cette paroi réelle (étude des phénomènes de diffusion thermique dans les corps poreux et dans les canalisations à vide ).

Pression

On peut faire un calcul assez simple de la pression dans un gaz en définissant celle-ci comme la force par unité de surface exercée sur une paroi. Du point de vue de la théorie cinétique, cette force est une valeur moyenne due à la succession de petites impulsions élémentaires produites par les collisions des molécules sur les parois. Si l’on suppose que la paroi est parfaitement plane et que les molécules rebondissent élastiquement sur celle-ci (fig. 11), on trouve que la force est normale à la paroi et, dans le cas simple d’un gaz dilué en équilibre thermodynamique à la température T, le calcul conduit, pour la pression p , à la loi des gaz parfaits :

Cependant, de manière générale, un gaz en mouvement est anisotrope et on ne peut pas considérer que la pression en un point soit un scalaire comme on le fait en hydrostatique. D’ailleurs, il est bien connu que la force exercée sur une paroi comporte alors, en plus de la composante normale, une composante tangentielle d’entraînement de la paroi. Mais, chose plus grave, la force exercée sur la paroi dépend a priori non seulement du gaz, mais aussi des propriétés physico-chimiques de la paroi: si l’on adopte le modèle de la figure 11, on en conclut que la force d’entraînement est nulle. En fait il n’en est rien, ce qui montre clairement qu’un tel modèle est trop simple et que, pour éviter de telles difficultés, la notion de pression doit être définie dans le volume même du gaz , indépendamment de la présence d’une paroi.

L’analyse faite par divers auteurs a démontré que la pression totale est un tenseur du deuxième ordre p. La quantité 暴 . p, divergence de ce tenseur, joue le rôle d’une force par unité de volume appliquée au fluide: p se compose de deux parties de natures différentes: une pression cinétique liée à l’agitation thermique et une pression dite intermoléculaire liée aux interactions entre molécules.

Le tenseur de pression cinétique se calcule à partir de la fonction de distribution f ¹ par la formule: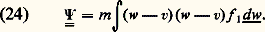

Comme le montre cette formule, c’est une mesure de l’agitation thermique, c’est-à-dire des écarts des vitesses w par rapport à la vitesse de fluide v; la pression cinétique serait nulle dans un faisceau parfaitement ordonné où toutes les molécules auraient la même vitesse w = v. Dans un gaz isotrope, la pression cinétique est un scalaire (plus précisément un tenseur diagonal unitaire), et l’on peut alors poser par définition:

^c est la température cinétique. Dans un gaz en équilibre thermodynamique, ^c se confond avec la température thermodynamique.

Le tenseur de pression intermoléculaire se calcule à partir de la densité double n ¹² et de la force d’interaction X¹² (force exercée par une molécule placée au point 2 sur une molécule placée au point 1) par la formule générale: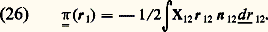

Dans un gaz isotrope , la pression intermoléculaire est un scalaire et peut se déduire du potentiel d’interaction 﨏(r ) (r = |r¹²|) par la formule:

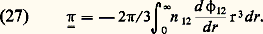La pression totale p étant la somme 切= + 神=, il est intéressant de comparer les deux termes de cette somme; on trouve alors que, dans un gaz dilué , la pression cinétique est dominante , la pression intermoléculaire n’est qu’une faible correction. En d’autres termes, la pression cinétique 切= est une généralisation de la loi des gaz parfaits au cas des gaz hors d’équilibre thermodynamique et anisotropes. La pression intermoléculaire est, dans les mêmes conditions, une généralisation des corrections dites de gaz réel ou de Van der Waals (appelées parfois aussi pression interne ). Cette correction peut être positive ou négative selon les propriétés des interactions moléculaires. Dans le cas d’un gaz isotrope, la formule (27) montre que 神 est positif si la loi d’interaction est répulsive à toute distance.

Flux de chaleur

Le tenseur flux de chaleur Q (tenseur du troisième ordre) peut être défini comme le quatrième «moment» de f ¹ (n , v, 切

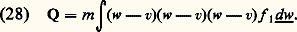On utilise souvent aussi une quantité un peu plus simple, le vecteur flux de chaleur:

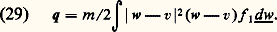Taux de réaction

Lorsque les énergies des molécules sont assez élevées, elles peuvent, par des collisions inélastiques, effectuer divers types de réaction. On appelle taux d’une certaine réaction j le nombre de réactions produites par unité de volume et par unité de temps. Ce taux dn ^j/dt se calcule à partir de la section efficace 靖^j de cette réaction et des fonctions de distribution des particules 1 et 2 qui réagissent. Jusqu’à maintenant n’ont été considérés que des gaz purs constitués d’une seule espèce de molécules; pour le calcul des taux de réactions, il est nécessaire en général de considérer un mélange gazeux constitué de particules 1 caractérisées par leur fonction de distribution simple f ¹ et de particules 2 caractérisées par leur fonction de distribution simple f ² (cela n’exclut cependant pas le cas d’un gaz pur où des réactions «symétriques» correspondant à 1 令 2 peuvent se produire). Pour effectuer le calcul, on remarque que les deux distributions f ¹ et f ² sont équivalentes à un ensemble de faisceaux élémentaires qui se croisent : à chacun de ces couples de faisceaux on peut, en considérant le mouvement relatif, appliquer la relation (10). On obtient ainsi, tout calcul fait pour le taux d’une réaction j , la relation:

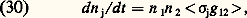avec: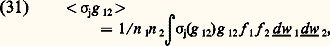

où g ¹² = |w¹ 漣 w²| est la vitesse relative. Dans certains cas, on définit une fréquence de collisions réactives (nombre de réactions par unité de temps et par particule initiale), qui, par exemple, pour les particules 1 s’écrit:

4. Propriétés des gaz en équilibre thermodynamique

Lorsqu’un gaz, enfermé dans un récipient qui constitue un thermostat de température T, est abandonné à lui-même, son état statistique microscopique tend, au bout d’un certain temps, vers un état parfaitement bien déterminé. Cet état d’équilibre thermodynamique est caractérisé par les propriétés suivantes:

1. La fonction de distribution simple est: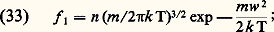

on l’appelle fonction de distribution de Maxwell-Boltzmann ou plus simplement fonction de distribution maxwellienne. Dans cette formule, m est la masse des molécules et k la constante de Boltzmann:

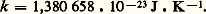La distribution maxwellienne est isotrope; de ce fait, on considère souvent la fonction de distribution des valeurs absolues des vitesses f ¹ = 4 神 w ² f ¹; les variations de f ¹ en fonction de w sont représentées schématiquement sur la figure 12: la courbe passe par un maximum pour une certaine vitesse w ⁰ appelée vitesse la plus probable :

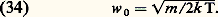On définit aussi deux autres moyennes légèrement différentes:

– La vitesse moyenne (moyenne de |w|):

– La vitesse quadratique moyenne (son carré est la moyenne de w ²):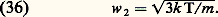

Cette dernière formule montre que l’énergie cinétique moyenne est égale à 3 k T/2, résultat qu’on rattache à une règle générale dite d’équipartition de l’énergie qui s’énonce ainsi:

Dans un système en équilibre thermodynamique, chacun des éléments du système possède une énergie moyenne d’agitation thermique Nk T/2, où N est le nombre des degrés de liberté de cet élément. Cette règle s’applique, à la seule condition que les effets quantiques soient négligeables, ce qui est le cas ici pour les trois degrés de liberté de translation d’une molécule, lesquels ne sont pas quantifiés.

2. La densité dans l’espace des phases est donnée par la formule de Gibbs :

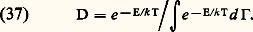Dans cette formule, le numérateur est le terme significatif; le dénominateur n’est qu’une constante de normalisation choisie de façon que l’on ait 咽D d 臨 = 1. E est l’énergie totale du gaz. Si l’on suppose fixée la composition chimique de celui-ci (c’est-à-dire si on néglige les collisions inélastiques et les changements d’état interne des molécules qui peuvent en résulter), on peut écrire E sous la forme: E = E^w + E^r, où E^w est la somme des énergies cinétiques des molécules et E^r la somme de leurs énergies potentielles. On peut en conclure que D se factorise alors:

où M¹, M², ..., M^N sont des fonctions maxwelliennes normalisées à l’unité; la factorisation de D est donc complète en ce qui concerne les vitesses; elle ne peut par contre se faire en ce qui concerne les positions, et ce à cause des forces d’interaction entre particules: le calcul des corrélations de position à partir de la formule (37) par la méthode régressive est en fait un problème difficile de la théorie cinétique des fluides.

5. Équations cinétiques

Pour étudier les états d’un fluide en dehors de l’état d’équilibre thermodynamique, il faut écrire les équations d’évolution des différentes grandeurs D, f ¹, f ¹², ..., à partir des équations de la mécanique.

Équation de Liouville

L’équation la plus fondamentale est celle qui décrit l’évolution de la densité D dans l’espace des phases. De manière tout à fait générale, on montre que cette équation s’écrit sous une forme particulièrement simple, lorsque l’espace des phases où D est défini est constitué à partir de variables q ⁱ et p ⁱ canoniquement conjuguées au sens de Hamilton. Dans ces conditions, on montre qu’un élément de volume quelconque de l’espace se conserve au cours de l’évolution dynamique du système (théorème de Liouville ) et que l’équation d’évolution de D (équation de Liouville ) s’écrit: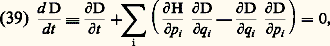

où H est l’hamiltonien du système. En pratique, dans la théorie cinétique des gaz, on considère généralement des particules non relativistes interagissant par des forces centrales; dans ces conditions, les variables rⁱ et m wⁱ sont conjuguées et l’équation de Liouville dans l’espace (rⁱ, wⁱ) s’écrit:

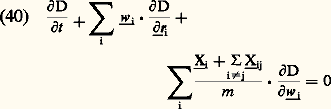où Xⁱ est la force d’origine extérieure agissant éventuellement sur la molécule i et X^ij la force d’interaction exercée par la molécule i .

Système d’équations de B.B.G.K.Y. (équations de la hiérarchie)

Par application de la méthode régressive, on peut obtenir, à partir de (40), les équations d’évolution des fonctions de distribution f ¹, f ¹², ... On obtient le système: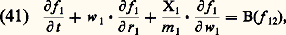

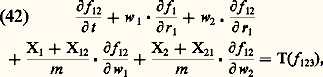avec: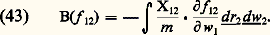

Malheureusement, les équations (41), (42), ... sont couplées de proche en proche: l’équation déterminant f ¹ contient f ¹², celle qui détermine f ¹² contient f ¹²³, etc. Si donc on s’arrête à un nombre fini d’équations, on a a priori un système indéterminé. Pour décrire complètement l’évolution du système, il faut en principe utiliser un système infini d’équations couplées analogue à (41) et (42). Ce système infini est appelé système B.B.G.K.Y., du nom des premiers auteurs qui l’ont considéré (Born, Bogolioubov, Green, Kirkwood, Yvon). La recherche d’approximations permettant d’arrêter le système B.B.G.K.Y. après une ou deux équations constitue un des problèmes fondamentaux de la théorie cinétique des fluides, connu sous le nom de problème de la fermeture du système d’équations de B.B.G.K.Y.

Équation de Boltzmann

Dans un gaz dilué constitué de molécules neutres, les forces d’interaction sont à courte portée, et la portée de ces forces est nettement inférieure à la distance moyenne entre les molécules. On en conclut que les collisions ternaires sont négligeables et qu’entre deux collisions binaires les trajectoires des molécules sont des segments de droite (qui peuvent être légèrement courbés par une force d’origine extérieure). Dans ces conditions on peut faire sur le terme B(f ¹²) de l’équation (43) des approximations qui conduisent à l’écrire sous la forme:

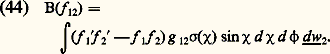Sous cette forme, l’équation (41) est appelée équation de Boltzmann. L’intégrale (44) y définit l’effet des collisions ; c’est une intégrale quintuple où les variables d’intégration sont les paramètres définissant la collision (w² vitesse de la molécule cible avant le choc, 﨑 et 﨏: angles définis sur la figure 1); f ¹ et f ² désignent les valeurs de la fonction de distribution pour les vitesses w¹ et w² avant le choc; f ¹ et f ² signifient ces mêmes grandeurs, mais pour les valeurs w¹ et w² des vitesses après le choc.

Le terme w ¹(face=F0019 煉f¹/ 煉r¹) qui apparaît dans (41) représente la contribution des effets de diffusion thermique à la variation de f ¹; ce terme n’existe que dans un gaz non homogène. Si l’on se reporte par exemple à la figure 9, il exprime le fait que sur la frontière de la bouffée, c’est-à-dire là où le gradient 煉f¹/ 煉r¹ est important, le simple effet des vitesses thermiques w¹ fait évoluer la fonction de distribution en un point donné.

Dans un gaz homogène et en l’absence de force extérieure, l’équation de Boltzmann s’écrit simplement:

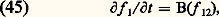le terme de collision B ayant la forme explicitée en (44). Sur cette équation, on peut vérifier les deux propriétés suivantes:

– L’équation de Boltzmann admet pour solution stationnaire toute fonction de distribution maxwellienne.

– Si, partant d’un état initial quelconque, on abandonne le gaz à lui-même, la fonction f ¹ tend vers la distribution maxwellienne d’équilibre: c’est ce qu’on appelle un phénomène de relaxation. Ce phénomène met en évidence un comportement irréversible du fluide. On peut vérifier au contraire que l’équation de Liouville est réversible par rapport au temps: on en conclut que l’irréversibilité s’introduit quand on se contente d’une description partielle du fluide, comme celle fournie par f ¹ qui ne contient qu’une partie de l’information. Cependant il s’agit là d’un des paradoxes délicats de la théorie cinétique.

6. Équations hydrodynamiques

Régimes de fluide quasi continu et régimes moléculaires

De manière générale, il est intéressant, dans toute expérience faisant intervenir un gaz, de comparer les dimensions du récipient contenant le gaz avec le libre parcours moyen 漣 des molécules de ce gaz entre deux collisions. Ce libre parcours moyen est toujours donné par la formule:

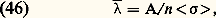où A est une constante sans dimension voisine de l’unité et 麗 靖 礪 une valeur moyenne de la section efficace totale de collision; les valeurs exactes de 麗 靖 礪 et de A dépendent de la forme de la fonction de distribution f ¹ et de la nature des interactions moléculaires qui interviennent (si le gaz est assez froid, les collisions dominantes sont élastiques, mais 靖 peut avoir, comme nous l’avons vu, des lois de variations en fonction de g très différentes). Quoi qu’il en soit, ces diverses difficultés n’entraînent en général sur 漣 qu’une incertitude d’un facteur 1 à 5. Dans ces conditions, si l’on appelle d une dimension caractéristique du récipient, on peut distinguer deux régimes très différents:

– Les régimes de fluide quasi continu correspondent au cas 漣 廉 d ; l’allure des trajectoires des molécules est alors représentée sur la figure 13 a. On voit que les molécules subissent presque uniquement des collisions entre elles, et très rarement des collisions contre les parois. Les parois joueront un rôle relativement faible; elles entourent un nuage de molécules qui interagissent essentiellement entre elles et qui semblent constituer un fluide quasi continu.

– Les régimes moléculaires correspondent au cas opposé d 廉 漣; les trajectoires des particules ont l’aspect représenté sur la figure 13 b. On voit que les collisions entre deux molécules à l’intérieur de l’enceinte sont très rares. Les molécules vont essentiellement d’une paroi à l’autre; l’action des parois pourra être prépondérante dans les propriétés du dispositif. D’autre part, on ne peut pas parler d’une masse de fluide située à l’intérieur de l’enceinte, on dit que le dispositif fonctionne en régime moléculaire.

Pour pouvoir déterminer rapidement le cas dans lequel on se trouve en pratique, il est commode de se rappeler les ordres de grandeur des libres parcours moyens dans des conditions typiques: lorsque la pression est égale à 10^-4 millimètre de mercure, le libre parcours moyen est de l’ordre de un mètre; on sera alors en général en régime moléculaire. Comme d’autre part le libre parcours moyen est inversement proportionnel à n , c’est-à-dire à la pression, on en déduit que, à la pression atmosphérique, les libres parcours moyens sont de l’ordre du dixième de micron, de sorte qu’on a en général à ce moment-là un régime de fluide quasi continu.

Équations de transport

Pour étudier un fluide en régime moléculaire, on a besoin en général du formalisme de la théorie cinétique. Par contre, en régime de fluide quasi continu, on peut essayer d’éviter ce formalisme qui est souvent trop lourd. Pour décrire l’évolution du fluide on doit alors utiliser des équations macroscopiques qui contiennent les grandeurs n, v, 切=, Q... Ces équations hydrodynamiques sont souvent appelées équations de transport , car on peut les obtenir à partir de l’équation de Boltzmann par le procédé général suivant: on multiplie ladite équation par une quantité A qui peut être en général fonction de r, w et t , et on intègre sur l’espace des vitesses w. On obtient ainsi l’équation de transport de la grandeur A. Les trois premières équations hydrodynamiques correspondent à A = 1, m w, m |w 漣 v|² et s’écrivent:

– Équation de conservation des molécules :

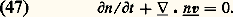– Équation de transport de la quantité de mouvement (équation fondamentale de l’hydrodynamique):

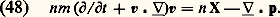– Équation de transport de la chaleur :

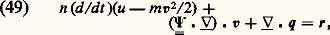avec: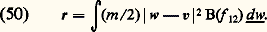

Ces équations sont écrites en supposant que le fluide est un gaz pur. Dans l’équation (47), le deuxième membre nul exprime le fait que les collisions ne changent pas le nombre de molécules (pas de collisions inélastiques ). Dans l’équation (48), équation de Newton appliquée à un fluide, X désigne la valeur moyenne (sur l’espace w) de la force appliquée aux molécules; dans les gaz neutres ce terme est en général négligeable; on voit par ailleurs que le terme 漣 暴 漣 . p divergence (changée de signe) de la pression totale joue le rôle d’une force par unité de volume. Dans l’équation (48), face="EU Upmacr" désigne l’énergie cinétique moyenne des particules; cette équation peut s’écrire aussi sous une forme tensorielle plus générale (équation de transport de la pression cinétique) en posant:

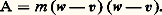Les équations de l’hydrodynamique posent comme le système B.B.G.K.Y. un problème de fermeture parce qu’elles constituent un système indéterminé (l’équation qui détermine n contient v, celle qui détermine v contient 切, etc.). En principe, on pourrait écrire un système infini d’équations hydrodynamiques, couplées ainsi de proche en proche; mais celui-ci serait au moins aussi lourd à manier que l’équation de Boltzmann (à laquelle il serait d’ailleurs équivalent). Pour fermer le système des équations hydrodynamiques après un nombre fini d’équations, il faut utiliser des approximations qui tiennent compte de situations physiques particulières qui peuvent se présenter. Les approximations les plus fréquemment utilisées sont les suivantes:

– L’approximation des faisceaux ordonnés , qui ne garde que les deux premières équations hydrodynamiques en négligeant la pression cinétique 切=, c’est-à-dire l’agitation thermique des particules. Dans un faisceau de particules neutres assez diluées, la pression interparticulaire est alors également négligeable. Cependant cette approximation est également utilisée dans les faisceaux de particules chargées et dans les plasmas (approximation des plasmas froids); dans ces fluides, le terme 暴 size=1^漣 . 神 漣 n’est pas alors forcément négligeable, mais il est proportionnel au champ électrique de charge d’espace E qui est déterminé par l’équation de Poisson.

– L’approximation des écoulements adiabatiques , qui garde les trois premières équations hydrodynamiques, en supposant, pour fermer le système, que le terme 暴 . q est nul. Cette approximation est utilisée (conjointement avec l’hypothèse d’une pression scalaire) pour décrire la propagation des ondes acoustiques dans les gaz.

– L’approximation de Navier-Stokes , dans laquelle on suppose que les collisions sont très importantes et que f ¹ est, en chaque point, presque maxwellienne. Une solution approchée de l’équation de Boltzmann permet alors d’exprimer p et q en fonction des gradients de vitesse et de température au moyen des formules:

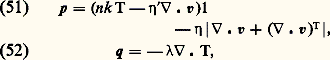où figurent trois coefficients de transport: 兀, 兀 , coefficients de viscosité;, coefficient de conductibilité thermique; 1 désigne le tenseur unitaire et ( 暴 . v)^T le tenseur transposé de 暴 . v.

Coefficients de transport

Les coefficients de transport apparaissent au niveau des équations macroscopiques comme des propriétés intrinsèques du fluide considéré. En fait ces coefficients peuvent être calculés à partir des lois d’interaction entre molécules en utilisant les méthodes de la théorie cinétique. Ces calculs sont souvent assez compliqués et l’on ne citera ici que les expressions élémentaires obtenues pour 兀 et, en utilisant le modèle de boules de billard de diamètre D; on trouve:

On voit que ces deux coefficients croissent avec la température, comportement qui différencie très nettement les gaz des liquides (la viscosité des huiles diminue quand T croît).

7. Problèmes particuliers

Effets des rotations et des vibrations dans les gaz non monoatomiques

Dans tout ce qui précède, on a assimilé les molécules à des masses ponctuelles; en d’autres termes, on a admis que le mouvement d’une molécule était complètement défini par les variables rⁱ et wⁱ, qu’on peut considérer comme la position et la vitesse du centre de gravité de la molécule; on peut encore dire qu’on n’a tenu compte que de l’agitation thermique de translation des molécules. D’autre part, on a admis que les forces d’interaction étaient des forces centrales dérivant d’un potentiel 﨏(r ). Il est clair que ces hypothèses s’appliquent bien aux gaz constitués de molécules monoatomiques (gaz rares, vapeurs métalliques). Si l’on considère maintenant des gaz constitués de molécules diatomiques (H², ², ², ...) ou polyatomiques (CO², H²O, ...), la description utilisée ne constitue qu’une première approximation, certes très utile, mais qui doit être corrigée sur certains points, pour tenir compte des phénomènes suivants:

– Une molécule diatomique ou polyatomique est animée d’un mouvement de rotation autour de son centre de gravité; les énergies de rotation sont quantifiées, mais les quanta de rotation sont en général très faibles (de 10^-2 à 10^-5 eV) devant les énergies d’agitation thermique, de sorte que de nombreux niveaux de rotation sont excités; il en résulte, d’après le principe de correspondance, qu’une description classique des rotations moléculaires est une assez bonne approximation (cf. mécanique QUANTIQUE).

– Une molécule diatomique ou polyatomique est animée d’un mouvement de vibration des divers atomes la constituant; dans les molécules diatomiques, la vibration se produit selon l’axe des deux noyaux; dans les molécules polyatomiques, il existe des modes propres de vibration qui dépendent de la structure des molécules. Les quanta de vibration sont plus élevés que ceux de rotation; pour les molécules stables ils sont, à la température ordinaire, nettement supérieurs aux énergies d’agitation thermique; dans ces conditions, les molécules du gaz restent toutes dans leur niveau fondamental de vibration. À haute température, les niveaux de vibration peuvent au contraire être excités, et les collisions entre molécules peuvent devenir inélastiques vis-à-vis de ce phénomène d’excitation des vibrations.

– Les molécules diatomiques ou polyatomiques n’ayant pas la symétrie sphérique, la force d’interaction entre deux molécules n’est évidemment pas une force centrale; elle dépend de l’orientation relative des deux molécules. Ce sont de telles forces non centrales qui permettent des échanges d’énergie de rotation entre deux molécules lors d’une collision.

Si l’on se contente d’étudier l’équilibre thermodynamique , on peut décrire sans trop de difficultés l’état du gaz, en utilisant les méthodes de la mécanique statistique quantique ; pour cela, on considère chaque niveau quantifié j de vibration ou de rotation d’une molécule comme constituant une espèce distincte de particule, de densité n ^j (chacune de ces espèces possède une distribution maxwellienne des vitesses de translation). La répartition des molécules entre les différents états j est donnée par la formule de Gibbs quantique: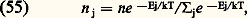

où n est la densité totale des molécules, et E^j l’énergie d’excitation de l’état j . Lorsque k T est très supérieur aux premières énergies d’excitation E^j, il en résulte que de nombreux niveaux d’énergie sont occupés, et l’on peut vérifier que les molécules du gaz possèdent une énergie cinétique moyenne de rotation égale à 2(k T/2) et, pour les gaz diatomiques, une énergie moyenne de vibration égale à k T/2 conformément à la règle d’équipartition de l’énergie.

Mais on peut vouloir étudier des états hors d’équilibre thermodynamique : phénomènes de relaxation , phénomènes de transport. Un exemple simple de la première catégorie est fourni par le passage d’une onde de choc à travers un gaz diatomique. Le passage du front de l’onde de choc produit une élévation immédiate de l’énergie de translation et de rotation des molécules; l’énergie de vibration, au contraire, n’est tout d’abord pas modifiée, mais le front de l’onde de choc est suivi d’un phénomène de relaxation relativement lent, au bout duquel les énergies de translation et de rotation ont diminué, et l’énergie de vibration augmenté, de façon que l’on atteigne un équilibre satisfaisant à la règle d’équipartition de l’énergie.

Pour étudier de tels problèmes, il faudrait pouvoir écrire des équations cinétiques qui tiennent compte de tous les degrés de liberté des molécules. Il s’agit là d’une question extrêmement difficile, encore mal résolue à l’heure actuelle.

Théorie cinétique des liquides

Une théorie cinétique exacte des liquides présente de grandes difficultés pour les raisons suivantes:

– Les hypothèses de base de la théorie cinétique des gaz (pas de collisions ternaires, collisions binaires séparées par des parcours libres) ne sont plus valables; de ce fait la fermeture du système B.B.G.K.Y. est plus difficile à étudier et, en particulier, l’équation de Boltzmann n’est pas valable;

– Bien que le problème précédent puisse être résolu formellement, l’obtention de résultats quantitatifs certains reste difficile en raison des trop grandes incertitudes que présentent encore les connaissances actuelles en ce qui concerne les forces d’interaction à courte portée.

Quelques théories approchées ont cependant pu être faites notamment sur l’équation d’état des liquides.

Théorie cinétique des plasmas

Un plasma est un fluide constitué de particules chargées ^{[cf. PLASMAS]}. Ici, on notera seulement deux propriétés fondamentales:

– Dans un plasma, une particule est, en général, en interaction effective avec un grand nombre d’autres; la notion de collision binaire qui sert de base à la théorie cinétique des gaz neutres ne permet pas de décrire les propriétés essentielles des plasmas;

– Les plasmas assez chauds et peu denses s’apparentent à l’état gazeux; les plasmas denses et moins chauds, à l’état liquide. La séparation entre ces deux familles est exprimée par la relation:

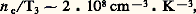où n ^e est la densité électronique et T la température.

Encyclopédie Universelle. 2012.